6. Maths4ML: Determinants & Eigenvectors

📅 2025-12-27 | #Maths for ML

Matrices are opaque

As established in last blog on matrices, they are machines which transforms a vector inputed to them. But any random matrix doesn't reveal what it is doing to data. To find out the DNA of the matrix, these 2 tools are needed :

Determinant : tells how much space is expanding or shrinking.
Eigen Vectors : tells along which line the stretching is happening.

Determinant (Scaling Factor)

To get the geometric intuition, let a unit square be sitting at the origin $(0, 0)$ . Area of the square is 1. When a matrix (linear transformation) is applied to this space, the grid line warp. The square will stretch into a long rectangle, skew into a diamond or even shrink into dot.

Determinant is the new area of the square.

Det = 2 : Space is stretching. Area of square doubles.
Det = 0.5 : Space is contracting. Area is halved.
Det = 1 : Shape might change. Area remains the same.

Singular Matrix

A matrix whose determinant = 0. This means the area of square becomes 0. This means the square is squashed completely flat into a single line or even a point.

This matrix which collapses the space is called Singular Matrix.

This matrix destroys information. When the square is squashed into a line, all information about how the original square looked like is lost. This process is irreversible.

Thus, singular matrix (matrix with det = 0) is non-invertible.

For a $2 \times 2$ matrix $A$ :

[a c b d]

The determinant is :

det (A) = a d - b c

The determinant is the factor by which the linear transformation scales area.

Derivation of Determinant

A = [a c b d]

This transforms the basis vectors into 2 new vectors :

Vector 1 : $v_{1} = (a, c)$
- Moves $a$ steps right, $c$ steps up
Vector 2 : $v_{2} = (b, d)$
- Moves $b$ steps right, $d$ steps up

These 2 vectors will form a parallelogram. Det is the area of this parallelogram.

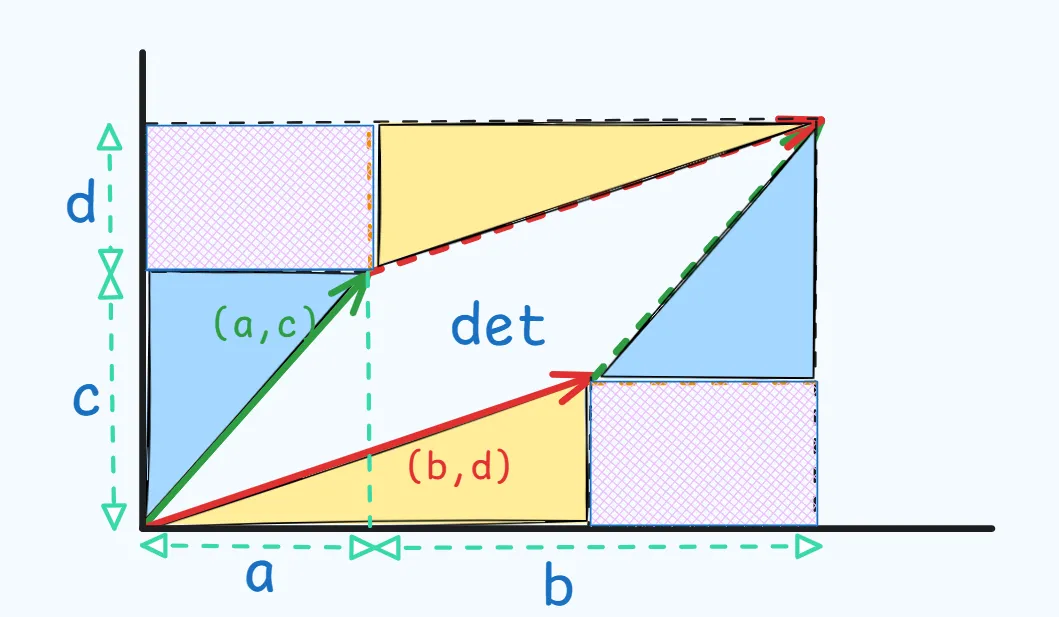
2D matrix determinant derivation

To find the area of the rectangle, subtract the area of the big box and the empty spaces surrounding the parallelogram.

As can be observed from the figure, area of big box = $(a + b) (c + d)$ .
The waste area consist of 2 of each of the blue & yellow triangle and the 2 pink rectangles.
- Their combined area = $(a \times c) + (b \times d) + (2 b c)$

Thus,

det (A) = (a + b) (c + d) - (a c + b d + 2 b c)

= (ab + a d + b c + b d) - a c - b d - 2 b c

= a d + b c - 2 b c

det (A) = ad - bc

Why determinant is the scaling factor?

The term $a d$ represents scaling along the main axes based on the original basis vectors.

The term $b c$ represents the twist or shears that interfere with the area.

So subtraction of the twist from stretch gives the true scaling factor.

Negative Determinant

It signifies that the universe has been flipped over. This means that the vectors are arranged in a clockwise manner.

A = [2002] A^{'} = [0220]

$A$ is the standard orientation (counter-clockwise) ans hence its determinant is positive.
$A^{'}$ is the swapped orientation (clockwise) ans hence its determinant is negative.

Thus, negative determinant just shows that the orientation has flipped.

Deteminant Drag

Drag the red and green basis vectors to change the matrix value. These vectors represent the columns of the transformation matrix.

Blue Square : Positive determinant (normal orientation)
Purple Square : Negative determinant (flipped orientation)
Collapsed Line : When determinant ≈ 0, the square flattens completely

There are also pre-existing presets for the transformation matrix.

Eigen Vectors (Stubborn Vectors)

Let there is a paper or a grid with some vectors (arrows) on it, and the paper is stretched from left and right side horizontally.

A vector pointing $45\degree$ will tilt and will be pulled horizontally.
The vector which was pointing perfrectly horizontally (eg. $\hat{i}$ ) will not tilt. It will just get longer.
The vector which was pointing perfrectly vertically (eg. $\hat{j}$ ) will also not tilt.

Eignen vectors are these stubborn arrows. These vectors stay on the same path even when other vectors get knocked off their path when a matrix transformation is applied. They don't change direction but only get scaled.

Eigenvector ( $v$ ) : The vector that refuses to rotate.
Eigenvalue ( $λ$ ) : The number describing how much the vector is stretched.

Eigenvectors is like the skeleton of the matrix. It reveals the principle axis along which the transformation is acting.

A v = λ v

$A v$ : Take the vector $v$ and transform it with matrix $A$ .
$λ v$ : Take the original vector $v$ and scale it by $λ$ .
The transformation didn't change the direction. It acted exactly like scalar multiplication.

Characteristic Equation

To find the eigen vectors, rearrange the above equation :

A v - λ v = 0

Factoring out $v$ :

(A - λ I) v = 0

If the matrix ( $A - λ I$ ) is ivertible, then the only solution will be $v = 0$ . For a non-zero vector $v$ that solves this equation, the matrix ( $A - λ I$ ) will have to squash the vector-space (send the non-zero vector to zero). This means the determinant of the matrix must be 0.

det (A - λ I) = 0

Solved Example of finding eigen vectors and eigen values

A = [4213]

Solving the Characteristic equation using the above matrix : $det (A - λ I) = 0$ .

det ([4213] - [λ 0 0 λ]) = 0

det [4 - λ 2 1 3 - λ] = 0

(4 - λ) (3 - λ) - (1) (2) = 0

λ^{2} - 7 λ + 10 = 0

(λ - 5) (λ - 2) = 0

So the 2 eigenvalues are : $λ_{1} = 5$ and $λ_{2} = 2$ .

Solving the linear system $(A - λ I) u = 0$ for the vector $v = [x y]$ will give the eigen vectors.

$λ = 5$ : It will give $x = y$ . So any vector where $x$ equals $y$ is an eigenvector.
- Eigenvector 1 : $v_{1} = [11]$
$λ = 2$ : It will give $y = - 2 x$ .
- Eigenvector 2 : $v_{2} = [1 - 2]$

Relationship between trace & eigenvalues and determinant & eigenvalues

Trace : sum of the top-left to bottom-right diagonal.

λ_{1} + λ_{2} = Trace (A)

λ_{1} \cdot λ_{2} = det (A)

EigenVector Hunt

Red Arrow : input vecetor
Yellow Arrow : transformed vecetor
Green Arrow : When the input and transformed vector align, that is the eigen vector.

There are 3 presets for the transformation matrix.

Drag the input vector to find the eigenvector.

Rotation Matrix

[01 - 1 0]

This matrix rotates the grid $90\degree$ clock-wise

det (A - λ I) = - λ 1 - 1 - λ

λ^{2} + 1 = 0 ⟹ λ = \pm i

Hence, there are no real eigenvalues and hence no real eigenvectors.

Thus, it is not possible to find the eigenvector in Pure Rotation preset above.

Eigen Decomposition (Matrix Factorization)

Matrix $A$ 's eigen decomposition is :

A = P D P^{- 1}

$P$ : Eigenvector Matrix
- Take all the eigenvectors ( $v_{1}, v_{2}, \dots$ ) and put them together as the columns of a single matrix

P = ∣ v_{1} ∣ ∣ v_{2} ∣

$D$ : Eigenvalue Matrix
- This is a Diagonal Matrix.
  - All the off-diagonal values are 0.
- Put all the corresponding eigenvalues ( $λ_{1}, λ_{2}, \dots$ ) on the main diagonal.

D = [λ_{1} 0 0 λ_{2}]

$P^{- 1}$ : Inverse
- Inverse of the eigenvector matrix

Intuition of Eigen Decomposition

A matrix $A$ when applied to a vector may result in the the x-coordinate git mixed into the y-coordinate. Everything is coupled together. Eigenvectors are the Axes of Rotation. If we look at the world from the perspective of the eigenvectors, there is no mixing. There is only stretching.

Eigen Decomposition breaks the transformation (matrix) $A$ into 3 distinct moves :

$P^{- 1}$ (The Twist) :
- Change the viewpoint. Rotate the entire coordinate system so that the eigenvectors become the new x and y axes.
$D$ (The Stretch) :
- Now that we are aligned with eigenvectors, the transformation is just scaling along the axes. There is no more rotation or shearing.
$P$ (The Untwist) :
- We rotate the coordinate system back to the original standard orientation.

A dense matrix $A$ is like a diagonal matrix $D$ (which is computationally easier to use) that is "wearing a costume." The matrices $P$ and $P^{- 1}$ are just the process of taking the costume off and putting it back on.

Thus, it is also called Diagonalization, because the matrix $A$ is replaced with a diagonal matrix $D$ .

Why perform diagonalization ?

As established, $A = P D P^{- 1}$ .

A^{2} = (P D P^{- 1}) (P D P^{- 1})

A^{2} = P D (P^{- 1} P) D P^{- 1} = P D^{2} P^{- 1}

Similarly, $A^{100} = P D^{100} P^{- 1}$

$D^{100}$ is a lot easy to caluculate as it is a diagonal matrix. So, just take the power of the diagonal elements.

D = [2003] ⟹ D^{100} = [2^{100} 0 0 3^{100}]

Drawback

Standard Eigenvectors and Eigenvalues are strictly for square matrices.

$A v = λ v$ . The Output Vector must be parallel to the Input Vector.

For a Square matrix ($2\times2$) :
- Takes a 2D vector and outputs a 2D vector.
For a Rectangular matrix ($3\times2$) :
- Takes a 2D vector and outputs a 3D vector.
- It changes the dimension, but the result should have been same as a scalar multiplication and that means dimensions must not change.

And as in most real world problems, data is not a square (eg. 1000 rows (users) & 50 columns (features)).

For this reason SVD is used for any shape.

Coordinate Changer

This simulation visualizes the equation :

A^{t} = P D^{t} P^{- 1}

$A$ : transformation matrix in the standard (x, y) coordinates.
- It is often coupled, i.e., x affects y, y affects x causing shearing and rotation.
$D$ : diagonal matrix containing the Eigenvalues ( $λ_{1}, λ_{2}$ ).
- It represents pure stretching/shrinking with no rotation.

The eigen vectors are defined as :

v_{1} = [cos (θ) sin (θ)]

v_{2} = [- sin (θ) cos (θ)]

These 2 vectors are dynamically calculated using the slider Eigenvector Angle.

These 2 vectors are always perpendicular, thus forming a pure rotation matrix $P$ .

The matrix $A$ is not fixed in this simulation. For any point $v$ , the transformation is calculated using $A = P D P^{- 1}$ .

$P$ (Basis Change) : The matrix formed by the eigenvectors columns: $(cos θ sin θ - sin θ cos θ)$
$D$ (Diagonal Scaling) : The matrix containing eigenvalues: $(λ_{1} 0 0 λ_{2})$

Thus to calculate $A^{t}$ , (On Left Side) the sim computes :

A^{t} = P \cdot (λ_{1}^{t} 0 0 λ_{2}^{t}) \cdot P^{- 1}

$P^{- 1}$ : Takes the cross formed by the eigenvectors and rotate it to match the x,y axis shape.
$D$ : Stretches $x$ by $λ_{1}^{t}$ and $y$ by $λ_{2}^{t}$ .
$P$ : Rotates the world back to original angle.

On Right Side :

Let the Horizontal Axis be Eigenvector 1 ( $v_{1}$ ).
Let the Vertical Axis be Eigenvector 2 ( $v_{2}$ ).

So, because of the way the camera view is defined, the grid lines are the eigenvectors.

All the points on the smiley face undergo the respective transformation :

Left : Calculates $A^{t} v$ by doing the three-step dance ( $P D^{t} P^{- 1}$ ).
Right : The transformation is by only Diagonal matrix $D^{t}$ , because the camera is already "rotated" to align with the eigenvectors, we skip the rotation steps ( $P$ and $P^{- 1}$ ) entirely.
- So the transformation becomes just the scaling : v.x * lambda1 and v.y * lambda2.

With this, the post on determinants and eigenvectors, their geometric implications and how diagonalization works and simplifies the task is complete.