3. Maths4ML: Dot Product

Drawbacks of Rulers (Euclidean Distance)

Example :

There is data of 2 people listening to music :

	Person A	Person B
Time per day	5 hours (300 mins)	10 mins
jazz	270 mins (90%)	9 mins (90%)
pop	30 mins (10%)	1 min (10%)

When plotted on a graph where axes are min. of jazz & min. of pop, then person A & B are miles apart.

The Euclidean distance between them will be huge.

• It tells how much physical space separates these two points?

Thus according to Euclidean distance, A & B have completely different taste. But logically, their tastes are same only the magnitude is different.

To solve this problem of looking at magnitude or looking at directions, Shadows are used.

Shadow (Projection)

Let there be 2 vectors A and B. Let a light source is shining down from above on A, perpendicular to B and casts shadow of A on B.

The length of shadow tells how much of vector A goes in the direction of vector B.

Or it can also be conveyed as drawing a straight line from the tip of the top vector down so that it hits the bottom vector perpendicularly.

The angle between the vectors/arrow tells the cosine similarity.

• Vectors pointing is same directions will have angle of $0\degree$ : perfectly aligned.
• Vectors perpendicular to each other will have angle of $90\degree$ : unrelated.

Dot Product

To understand projections dot product and its geometric definition is helpful.

$$ \mathbf{a} \cdot \mathbf{b} = \sum a_i b_i = a_1b_1 + a_2b_2+\cdots+a_nb_n $$

Multiply matching coordinates and sum them up.

Geometric definition

$$ \mathbf{a} \cdot \mathbf{b} = |a||b| \cos(\theta) $$

So, dot product is basically Length of A x Length of B x Percentage of alignment ($\cos\theta$).

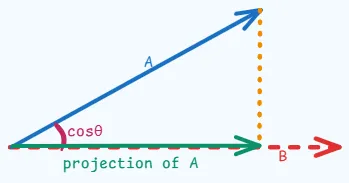
From trigonometry,

$$ \text{Projection Length} = |a| \cos(\theta) $$

It is saying, how much of a exists in the direction of b.

$$\mathbf{a} \cdot \mathbf{b} = \underbrace{|\mathbf{a}| \cos(\theta)}_{\text{Shadow}} \times |\mathbf{b}|$$ $$\mathbf{a} \cdot \mathbf{b} = (\text{Length of Shadow}) \times (\text{Length of Ground})$$

So, Dot Product is designed to measure the total impact of one vector moving along another.

Cosine Similarity

$$ \text{Cosine Similarity} = \cos(\theta) = \frac{\mathbf{a}\cdot \mathbf{b}}{|a||b|} $$

This comes directly from the geometric definition above.

The vectors get normalized by dividing by lengths. This turns vectors a & b into unit vectors. And now only their alignment is left to compare.

• Result +1.0: Perfect Match ($0\degree$).
• Result 0.0: Orthogonal / No Relation ($90\degree$).
  • Because $\cos(90\degree)=0$.
• Result -1.0: Exact Opposites ($180\degree$).

Shadow Caster

Drag the white arrow (vector A) or adjust the sliders to change its length and direction.

• The yellow line is the projection / shadow cast upon the green / ground vector.
• When the white arrow is straight up, shodow is gone and cosine similarity is 0, signifying orthogonality or independence.
• An obtuse angle or ($\gt 90\degree$) represents negative correlation

---

With this, dot product and its geometric meaning is covered.