5. Maths4ML: Matrices

📅 2025-12-25 | #Maths for ML

Matrices are Space Warpers

A matrix is not just a spreadsheet or a container for data. It is a function or a machine. Ab equation like $y = A x$ (in a Neural Network or linear regression, etc.), the matrix $A$ is a function or an agent that grabs the data vector ( $x$ ) and physically moves it, warps it and transforms it into a new position ( $y$ ).

Matrices can stretch space and collapse dimensions.

Matrix transforming the Basis Vectors

Let the basis vectors be denoted by :

$\hat{i}$ : $[1, 0]$ - A Green arrow pointing right.
$\hat{j}$ : $[0, 1]$ - A Red arrow pointing up.

The columns of a matrix tells exactly where these 2 arrows will land after transformation.

A = [30 - 1 2]

Column 1 $(3, 0)$ : The $\hat{i}$ basis vector now lives here from $(1, 0)$ .
Column 2 $(- 1, 2)$ : The $\hat{j}$ basis vector now lives here from $(0, 1)$ .
Every other point on the grid will follow the new grid lines (basis) formed by these 2 arrows.

So, for example a point $[2, 1]$ according to the old system would have meant to go 2 units of $\hat{i}$ and 1 unit of $\hat{j}$ , but now since these basis vectors point in different direction, the same vector $[2, 1]$ will point in a completely different direction.

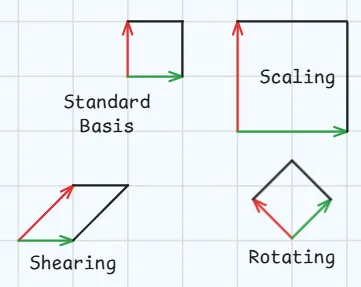
Fundamental Matrices

1. Scaling

Doubling the length of the green & red arrow will cause the matrix to zoom in on the data. For example :

[2002]

2. Rotation

Arrows stay the same in length but pivot $90\degree$, the matrix spins the entire world. The grid will remain square but tilted :

[01 - 1 0]

3. Shearing

If the bottom of a square if fixed and the top is pushed sideways. The square will turn into a parallelogram.

[1011]

Below image shows the exact matrices transformations as covered above.

Standard Matrix transformations (Scaling, Rotation & SHearing)

Matrix Vector Multiplication

[a c b d] [x y] = [a x + b y c x + d y]

This is Row-by-Column multiplication. It is computationally correct but it doesn't offer any intuition. This same thing can be represented as :

x \cdot [a c] + y \cdot [b d]

This is literally saying :

Take $x$ steps along the transformed Green Arrow (Column 1) and then take $y$ steps along the transformed Red Arrow (Column 2).

Matrix-Matrix Multiplication

A matrix-matrix multiplication like $C = A B$ using standard row-by-column method is a mess of numbers.

A better way is to look at matrix $B$ as a collection of columns (vectors).

A \times B = A \times [v_{1} ∣ v_{2}]

So now instead of one big operation it is just doing matrix-vector multiplication twice, once for each of the column of $B$ .

Column 1 of result : $A$ acts on the first column of $B$ .
Column 2 of result : $A$ acts on the second column of $B$ .

A [a c b d] B [x_{1} y_{1} x_{2} y_{2}] = C

Column 1 of matrix $C$ is the result of passing column 1 of $B$ through machine (matrix) $A$ :

Col 1 = x_{1} [a c] + y_{1} [b d]

Column 2 of matrix $C$ is the result of passing column 2 of $B$ through machine (matrix) $A$ :

Col 2 = x_{2} [a c] + y_{2} [b d]

So, finally Matrix $C$ is just these 2 results pasted side-by-side :

C = [(x_{1} [a c] + y_{1} [b d]) (x_{2} [a c] + y_{2} [b d])]

Thus,

The output columns of $C$ are literally just weighted sums of the columns of $A$ . The resulting shape must live inside the space defined by $A$ 's columns.

Matrix Multiplication is Function Composition

Matrix multiplication is simply chaining multiple machines.

y = A (B (x))

The vector $x$ is the raw material.

Machine $B$ is the first machine which transforms it.
Machine $A$ is the second machine which grabs the result of Machine $B$ and transforms it again.

Why MatMul is not commutative

Suppose 2 matrices $S$ & $R$ which stretch the $x$ -axis by 2 and rotate everything by $90\degree$ respectively.

S = [2001], R [0 - 1 10]

Scenario 1 : Stretch then rotate

$y = RS x$
Stretches left-right.
Rotates so that left becomes bottom & right becomes top.

Scenario 2 : Rotate then stretch

$y = SR x$
Rotates so that left becomes bottom & right becomes top.
Stretches the original top-bottom (which are now left-right).

Thus, even though the same operations are applied, the order changes everything. Thus, $A B \neq = B A$ .

Invertible Matrices

Chaining matrices to get back to from where we started.

Matrix $A$ is a Shear Right matrix.

A = [1011]

Matrix $B$ is a Shear Left matrix.

B = [10 - 1 1]

Therefore, $y = B A x$ will slant a square right and then push it back to the original shape.

Thus, $B = A^{- 1}$

B \times A = [1001] = I

$I$ is the identity matrix that does nothing.

Transpose

Mechanical definition is to swap the rows & columns.

A = [142536], A^{⊤} 123456

Co-variance

$X^{⊤} X$ is the similarity map of data $X$ . Let there be a dataset of 3 students consisting of their study time & score.

X = Student 1 Student 2 Student 3 = - 1 01 - 2 02

Column 1 : Blue vector is the study vector. $s = [- 1, 0, 1]$
Column 2 : Red vector is the score vector. $g = [- 2, 0, 2]$

X^{⊤} = [- 1 - 2 0012]

Now Row 1 is the study vector & Row 2 is the score vector.

Thus, $X^{⊤} X$ will become :

[Study Score] \cdot [Study Score] = [2448]

Cell (1,1) : Variance of the Study vector.
Cell (2,2) : Variance of the Score vector.
Cell (1,2) & (2,1) : Covariance of the Score & Study vectors.

[Variance(Study) Covariance(Score, Study) Covariance(Study, Score) Variance(Score)]

Diagonals: How spread out is this feature? (Variance)
Off-Diagonals: How much does Feature A look like Feature B? (Covariance/Similarity)

Symmetric Matrix

Matrix is equal to its own transpose. $A_{ij} = A_{ji}$

A = A^{⊤}

Let :

A = [1021]

This is an Asymmetric Matrix. If the input is a circle, this matrix will grab the top & slide it sideways. The result will be a oval but it will be smeared.

S = [2112]

This is a symmetric matrix. It will also stretch a circle but the resultant will be an ellipse with its major & minor axis perpendicular to each other.

Asymmetric Matrix : Might shear space, twist it, and squash it at weird angles.
Symmetric Matrix : It creates a shape where the axes of stretching are perpendicular.

Trace

The trace ( $Tr (A)$ ) of the matrix $A$ is sum of its diagonal elements.

In a matrix $A = [a c b d]$ :

Off diagonal elements :
- $c$ : tells how much $\hat{i}$ points Up into the y-axis.
- $b$ : tells how much $\hat{j}$ points Right into the x-axis.

They describe how much $x$ becomes $y$ and $y$ becomes $x$ .

Diagonal elements :
- $a$ : tells how much $\hat{i}$ stretches while staying along the x-axis.
- $d$ : tells how much $\hat{j}$ stretches while staying along the y-axis.

They describe the direct stretching.

So $Tr (A) = a + d$ tells how much the matrix pushing outward along the original grid lines.

The Trace ignores the mixing. It only asks: "On average, is the machine stretching things out or shrinking them in?"

Trace > 0 : Matrix is generally expanding the space.
Trace < 0 : Matrix is generally collapsing the space.
Trace = 0 : The expansion in one direction is perfectly cancelled by contraction in the other.

Range (Column Space)

Range of a matrix is the Span of its columns.

Span of a set of vectors is the set of all the vectors that can be formed by scaling & adding those vectors.

Thus, Column Space (Range) is the set of vectors that can be get by taking all possible linear combinations of its column vectors.

Range (A) = Span (Column 1, Column 2, ...)

Null Space

The null space (or kernel) of a matrix $A$ is the set of all vectors $x$ that satisfy the equation $A x = 0$ (the zero vector).

Rank

It is a single number which measures the dimension of the space. It tells the number of actual, non-redundant columns in a matrix.

A = [100111]

Column 3 = Column 1 + Column 2.
- Thus, there are only 2 dimensions as the third column is just a diagonal lying in the plane defined by the first 2 columns.
- Thus, Rank = 2.

The concept of dimensionality reduction is based on this fact to throw away the Fake dimensions and keep only the Rank dimensions (the true signals).

Thus,

Concept	Definition	Intuition
Columns	The vectors $v_{1}, v_{2}, \dots, v_{n}$ that make up the matrix $A$ .	The Raw tools, Arrows, some of which may be redundant
Span	The set of all possible linear combinations of a list of vectors: $S = {c_{1} v_{1} + \dots + c_{n} v_{n}}$ .	The Cloud. The total shape created by stretching and combining the raw tools in every possible way
Range (Column Space)	The subspace of outputs reachable by the linear transformation $f (x) = A x$ . Mathematically equivalent to the Span of the columns.	The Reach. When we view the matrix as a machine, the Range is the specific "territory" the machine can touch.
Basis	A minimal set of linearly independent vectors that spans a subspace.	The Skeleton. If you strip away all the redundant columns (the fake tools), this is the clean, efficient set of arrows left over that still builds the same Cloud.
Rank	The dimension of the Column Space.	The Score. A single number representing the "True Dimension" of the output. It tells how many useful dimensions exist in your data.

The Columns of the matrix generate a Span. When viewed as a function, this Span is called the Range. The smallest set of vectors needed to describe this Range is the Basis, and the count of vectors in that Basis is the Rank.

Space Warper

Modify the transformation matrix by dragging the basis vectors ( $\hat{i}$ and $\hat{j}$ ) or by changing the sliders values representing :

Transformation Matrix = [a c b d] = [1001]

Vector $[a c]$ represents $\hat{i}$ .
Vector $[b d]$ represents $\hat{j}$ .

When the green arrow aligns with red arrow, it signifies a dimension loss.

With this this post on matrices and their geometric implementation, types of matrices and different operations using matrices is completed.