2. ML: Linear Regression

Regression Problem

It is a statistical process for estimating the relationships between a dependent variable (outcome) and one or more independent variables (features).

• Input $X$ : Attribute variables or features (typically numerical values).
• Output $Y$ : Response variable that is aimed to be predicted.

Cyan: Goal is to estimate a function $f(X,\beta )$ such that $Y\approx f(X,\beta )$.

It is called linear regression because this relation is assumed to be linear with an additive error term $ϵ$ representing statistical noise.

---

Simple Linear Regression Formulation

For a single feature vector $x$, the regression models is defined as :

$$Y_i={\beta }_0+{\beta }_1{x}_i+{ϵ}_i$$

• $Y_i$ : observed response for $i$-th training example
• $x_i$ : input feature for the $i$-th training example
• ${\beta }_0$ : intercept (bias)
• $bet{a}_1$ : slope (weight)
• ${ϵ}_i$ : residual error

This represent the actual training dataset values.

---

The fitted values or the prediction is :

$${\hat{y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1{x}_i$$

---

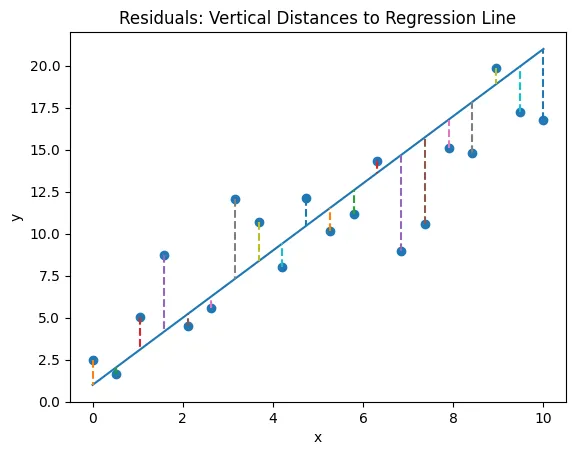
Ordinary Least Square (OLS)

It is the method to estimate the unknown parameters ($\beta$) by minimizing the sum of the squares of the differences between the observed dependent variables and the predicted ones by the liner function. Squared error penalizes large errors more than smaller ones.

Derivation of Sum of Squared Errors (SSE)

Residual Sum of Squares (SSE) cost function $L$ is defined as :

$$L({\beta }_0,{\beta }_1)=\sum _{i=1}^n{ϵ}_i^2=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2=\sum _{i=1}^n(y_i-({\beta }_0+{\beta }_1{x}_i){)}^2$$

Green: Goal is to : $min({\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2)$

To find the optimal ${\beta }_0$ and ${\beta }_1$, we take partial derivative w.r.t each parameter and set them to 0.

1. Derivative w.r.t ${\beta }_0$ :

To minimize, the derivative must be equal to 0 :

$$\frac{\partial L}{\partial {\beta }_0}=-2\sum _{i=1}^n(y_i-{\beta }_0-{\beta }_1{x}_i)=0$$

Since ${\beta }_0$ and ${\beta }_1$ are constants :

$$\sum _{i=1}^n{y}_i-n{\beta }_0-{\beta }_1\sum _{i=1}^n{x}_i=0$$

Dividing by $n$ :

$$\frac{1}{n}\sum _{i=1}^n{y}_i-\frac{1}{n}n{\beta }_0-\frac{1}{n}{\beta }_1\sum _{i=1}^n{x}_i=0$$ $$\bar{y}-{\beta }_0-{\beta }_1\bar{x}=0$$ $$\boxed{{\beta }_0=\bar{y}-{\beta }_1\bar{x}}$$

2. Derivative w.r.t ${\beta }_1$ :

$$\frac{\partial L}{\partial {\beta }_1}=-2\sum _{i=1}^n{x}_i(y_i-{\beta }_0-{\beta }_1{x}_i)=0$$

Substitue ${\beta }_0$ with $\bar{y}-{\beta }_1\bar{x}$ :

$$\sum _{i=1}^n{x}_i(y_i-(\bar{y}-{\beta }_1\bar{x})-{\beta }_1{x}_i)=0$$ $$\sum _{i=1}^n{x}_i(y_i-\bar{y}+{\beta }_1\bar{x}-{\beta }_1{x}_i)=0$$ $$\sum _{i=1}^n{x}_i((y_i-\bar{y})-{\beta }_1(x_i-\bar{x}))=0$$ $$\sum _{i=1}^n{x}_i(y_i-\bar{y})-{\beta }_1\sum _{i=1}^n{x}_i(x_i-\bar{x})=0$$

Rearranging :

$${\hat{\beta }}_1=\frac{{\sum }_{i=1}^n{x}_i(y_i-\bar{y})}{{\sum }_{i=1}^n{x}_i(x_i-\bar{x})}$$

---

Identity : $\sum (x_i-\bar{x})=0$ and same is true for $y_i,\bar{y}$.

Thus, numerator becomes :

$$\sum _{i=1}^n{x}_i(y_i-\bar{y})=\sum _{i=1}^n{x}_i(y_i-\bar{y})-\bar{x}\underset{=0}{\underbrace{(y_i-\bar{y})}}=\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$

And thus denominator becomes :

$$\sum _{i=1}^n{x}_i(x_i-\bar{x})=\sum _{i=1}^n(x_i-\bar{x})(x_i-\bar{x})=\sum _{i=1}^n(x_i-\bar{x}{)}^2$$

---

And finally the slope ${\beta }_1$ becomes :

$${\hat{\beta }}_1=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}$$

And in terms of covariance and variance :

$$\boxed{{\hat{\beta }}_1=\frac{Cov(X,Y)}{Var(X)}}$$

---

Sum of Squares Decomposition and $R^2$

To evaluate the goodness of fit, we decompose the total variability of the response variable.

1. SST (Total Sum of Squares) : Measures total variance in observed $Y$ :

$$SST=\sum _{i=1}^n(y_i-\bar{y}{)}^2$$

• real vs mean

2. SSR (Sum of Squares Regression) : Measures variance explained by the model :

$$SSR=\sum _{i=1}^n({\hat{y}}_i-\bar{y}{)}^2$$

• predicted vs mean

3. SSE (Sum of Squares Error) : Measures unexplained variance (residuals) :

$$SSE=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

• real vs predicted

These are related as :

$$SST=SSR+SSE$$

Coefficient of Determination ($R^2$)

$R^2$ represents the proportion of the variance for the dependent variable that's explained by an independent variable.

$$R^2=\frac{SSR}{SST}$$

Also,

$$1=\frac{SST}{SST}=\frac{SSR+SSE}{SST}=R^2+\frac{SSE}{SST}$$

• The best model will have $R^2=1$.

---

Correlation Coefficient ($r^2$)

For simple linear regression, $R^2$ is the square of Pearson Correlation Coefficient ($r$) :

$$r=\frac{Cov(X,Y)}{{\sigma }_X{\sigma }_Y}⟹R^2=r^2$$

---

Types of Errors

Different metrics are used for different purposes :

1. Mean Squared Error (MSE) :

$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

• Differentiable and useful for optimization.
• Heavily penalizes large outliers (squaring term).

2. Root Mean Squared Error (RMSE) :

$$RMSE=\sqrt{MSE}$$

• Same unit as the target variable $Y$, making it interpretable.

3. Mean Absolute Error (MAE) :

$$MAE=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|$$

• More robust to outliers than MSE, but not differentiable at 0.

---

Multiple Linear Regression

When multiple features are present like $x_1,x_2,\dots ,x_n$, the model becomes :

$${\hat{y}}^{(i)}=w_0+w_1{x}_1^{(i)}+\cdots +w_n{x}_n^{(i)}$$

Vector-Matrix representation

Add a bias term as $x_0=1$ for the intercept $w_0$ into the weight vector :

• Input Matrix $X$ : Dimensions $N\times (n+1)$

$$X=\left[\begin{array}{cccc}1& x_1^{(1)}& \dots & x_n^{(1)}\\ 1& x_1^{(2)}& \dots & x_n^{(2)}\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_1^{(N)}& \dots & x_n^{(N)}\end{array}\right]$$

• $x_i^{(j)}$ : $j$-th training example's $i$-th feature.

• Weight Vector $w$ : Dimensions $(n+1)\times N$

$$w=[w_0,w_1,\dots ,w_n{]}^T$$

• Target Vector $y$ : Dimensions $N\times 1$

The prediction can be written using the inner product for a single example or matrix multiplication for the whole dataset:

$$\underset{N\times 1}{\underbrace{\hat{Y}}}=\underset{N\times (n+1)}{\underbrace{X}}\cdot \underset{N\times 1}{\underbrace{w}}$$

---

Closed Form / Normal Form Equation

Green: To find the coefficient $w$, minimize the sum of squared error (SSE)

Define the cost function

Cost function (quantifies the error between a model's predicted outputs and the actual target values) :

$$J(w)=\underset{w^{\ast }}{\min }\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

• $w^{\ast }$ : optimal value of the parameter.

SSE = $\Vert y-\hat{y}{\Vert }^2$ which is equal to magnitude of the vector $y-\hat{y}$. Due to the fact that $\Vert z{\Vert }^2=z_1^2+\dots z_p^2=z^T\cdot z$ :

$$SSE=(y-\hat{y}{)}^T(y-\hat{y})$$

And since $\hat{y}=X\cdot w$

$$SSE=(y-Xw{)}^T(y-Xw)=J(w)$$

Thus,

$$J(w)=(y^T-(Xw{)}^T)(y-Xw)$$ $$J(w)=(y^T-w^T{X}^T)(y-Xw)$$

Solving this gives :

$$J(w)=y^{T}y-y^{T}Xw-w^T{X}^{T}y+w^T{X}^{T}Xw$$

The term $y^{T}Xw$ will give a scalar value of dimension ($1\times 1$). And because transpose of a scalar is equal, $y^{T}Xw=w^T{X}^{T}y$. Thus,

$$J(w)=y^{T}y-2w^T{X}^{T}y+w^T{X}^{T}Xw$$

Computing the gradient

To find the optimal $w$ that minimizes error, we calculate the gradient of $J(w)$ with respect to $w$ and set it to zero.

$$\frac{\partial J(w)}{\partial w}=\frac{\partial }{\partial w}(y^{T}y-2w^T{X}^{T}y+w^T{X}^{T}Xw)$$

• $\frac{\partial }{\partial w}(y^{T}y)=0$

  • Constant with respect to $w$

• $\frac{\partial }{\partial w}(-2w^T{X}^{T}y)=-2X^{T}y$

  • $w$ is our variable vector $(d\times 1)$.
  • $a=-2X^{T}y$ is a constant vector $(d\times 1)$ because it doesn't contain $w$.
  • The term $-2w^T{X}^{T}y$ can be rewritten as the dot product $w^{T}a$.
  • Rule: The derivative of a dot product with respect to one of the vectors is just the other vector.

$$\frac{\partial }{\partial w}(w^{T}a)=a$$

• $\frac{\partial }{\partial w}(w^T{X}^{T}Xw)=2X^{T}Xw$
  • $w$ is a vector.
  • $A=X^{T}X$ is a square matrix.
  • The expression $w^{T}Aw$ is called a Quadratic Form.
  • Rule: The derivative of a quadratic form ${\mathbf{x}}^{T}A\mathbf{x}$ depends on whether matrix $A$ is symmetric.

$$\frac{\partial }{\partial \mathbf{x}}({\mathbf{x}}^{T}A\mathbf{x})=2A\mathbf{x}$$

Another rule followed :

$$\frac{\partial Xw}{\partial w}=X^T$$

Thus, the final gradient becomes :

$$J(w)=-2X^{T}y+2X^{T}Xw=-2X^T(y-Xw)$$

Solving for $w$

Equating the gradient to 0 :

$$J(w)=-2X^T(y-Xw)=0$$ $$X^T(y-Xw)=0$$ $$w=\frac{X^{T}y}{X^{T}X}$$

Thus, the closed form or the normal form equation is :

$$\boxed{w=(X^{T}X{)}^{-1}{X}^{T}y}$$

Limitations

1. It requires $(X^{T}X)$ to be invertible, i.e., the features must not be perfectly correlated.
2. For larger data, computation required to compute the inverse will be too large.

---

Gradient Descent

When the normal equation becomes too computationally expensive, we use Gradient Descent : an iterative optimization algorithm.

Cost Funtion (Mean Squared Error Form)

$$J(w)=\frac{1}{2n}\sum _{i=1}^n(y^{(i)}-w^T{x}^{(i)}{)}^2$$

• The $1/2$ factor makes the derivative cleaner.

Update Rule

Update the weights by moving in the opposite direction of the gradient / negative gradient.

$$w_j:=w_j-\alpha \frac{\partial J(w)}{\partial w_j}$$

• $\alpha$ is the learning rate

The gradient for a specific weight $w_j$ is :

$$\frac{\partial J(w)}{\partial w_j}=\frac{1}{n}\sum _{i=1}^n(w^T{x}^{(i)}-y^{(i)})x_j^{(i)}$$

---

Types of Gradient Descent

Type	Description	Pros	Cons
Batch GD	Uses all N training examples for every update.	Stable convergence.	Slow for large datasets; memory intensive
Stochastic GD (SGD)	Uses 1 random training example per update.	Faster iterations; escapes local minima	High variance updates; noisy convergence
Mini-Batch GD	Uses a small batch (b) of examples per update.	Balances stability and speed.	Hyperparameter b to tune

---

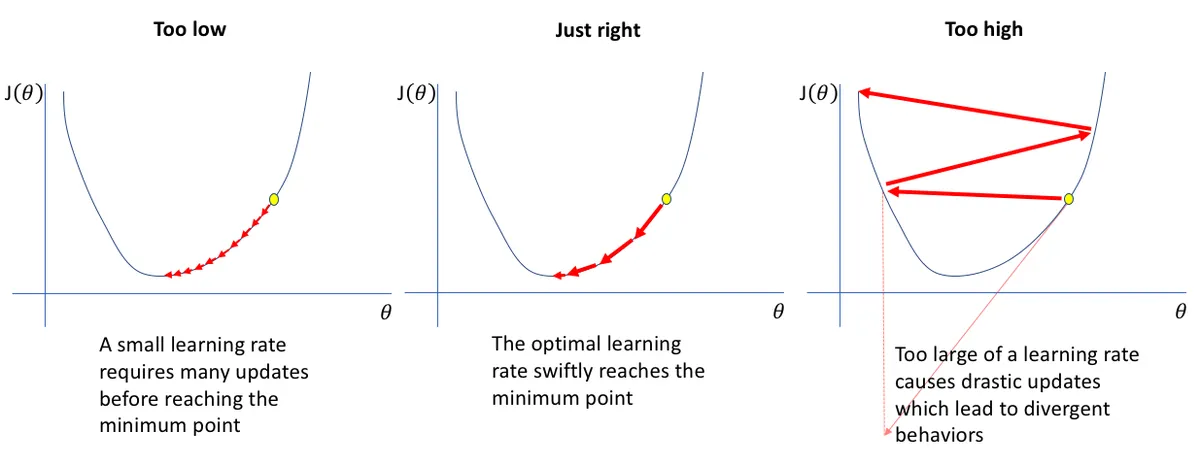
Learning Rate ($\alpha$)

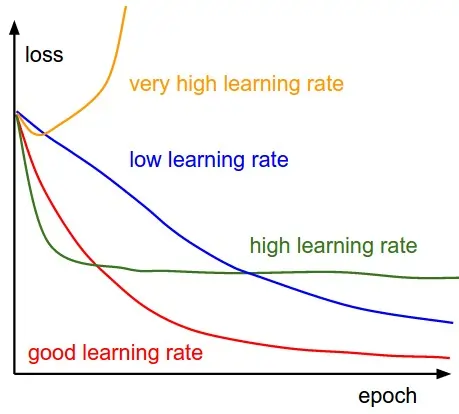
It is a critical hyperparameter that controls the step size taken towards a minimum of a loss function during optimization

• $\alpha$ too small: Convergence is guaranteed but very slow; requires many updates.
• $\alpha$ too large: The steps may overshoot the minimum, causing the algorithm to oscillate or diverge (cost increases).
• Optimal $\alpha$: Smoothly reaches the minima.

---

Worked out examples of Gradient Descent

• Problem : Fit : $y=w_0+w_{1}x$.

• Dataset :

  • Point 1: $(x^{(1)},y^{(1)})=(1,2)$
  • Point 2: $(x^{(2)},y^{(2)})=(2,4)$

• Initialization :

  • $w_0=0,w_1=0$
  • Learning Rate $\alpha =0.1$.

Batch Gradient Descent

It calculates gradient using sum over all points ($N=2$).

• ${\hat{y}}^{(1)}=0+0(1)=0$

  • Error : $0-2=-2$

• ${\hat{y}}^{(2)}=0+0(2)=0$

  • Error : $0-4=-4$

Gradients :

$$\frac{\partial J(w)}{\partial w_0}=\frac{1}{n}\sum _{i=1}^n(w^T{x}^{(i)}-y^{(i)})$$

• Because $x_j^{(i)}=1$ for $j=0$. Thus, :

$$\frac{\partial J}{\partial w_0}=\frac{1}{2}\sum _{i=1}^2({\text{Error}}^{(i)})\cdot x_0^{(i)}=\frac{1}{2}(-2(1)-4(1))=-3$$

---

$$\frac{\partial J(w)}{\partial w_1}=\frac{1}{n}\sum _{i=1}^n(w^T{x}^{(i)}-y^{(i)})x_1^{(i)}$$ $$\frac{\partial J}{\partial w_1}=\frac{1}{2}\sum (\text{Error}\times x)=\frac{1}{2}(-2(1)-4(2))=-5$$

Update :

$$w_0:=0-0.1(-3)=0.3$$ $$w_1:=0-0.1(-5)=0.5$$

Thus, the model after 1 epoch (1 complete pass through the dataset) is

$$y=0.3+0.5x$$

---

Stochastic Gradient Descent (SGD)

It updates after each example.

$$w_j:=w_j-\alpha \underset{\text{Gradient for single example}}{\underbrace{({\hat{y}}^{(i)}-y^{(i)})x_j^{(i)}}}$$

Iteration 1 :

• Pred : ${\hat{y}}^{(1)}=w_0(1)+w_1(x^{(1)})=0(1)+0(1)=0$

• $\text{Error}=({\hat{y}}^{(1)}-y^{(1)})=0-2=-2$

• Gradient for $w_0$ as $x_0=1$.

$$\frac{\partial J}{\partial w_0}=\text{Error}\times 1=-2$$

• Gradient for $w_1$ as $x_1=1$.

$$\frac{\partial J}{\partial w_1}=\text{Error}\times x^{(1)}=-2\times 1=-2$$

• Update :

$$w_0:=0-0.1(-2)=0.2$$ $$w_1:=0-0.1(-2)=0.2$$

Thus, the current model is : $y=0.2+0.2x$

Iteration 2

Use the updated weights from Iteration 1.

• Prediction : ${\hat{y}}^{(2)}=0.2(1)+0.2(2)=0.2+0.4=0.6$
• $\text{Error}=({\hat{y}}^{(2)}-y^{(2)})=0.6-4=-3.4$
• Compute gradients

$$\frac{\partial J}{\partial w_0}=-3.4\times 1=-3.4$$ $$\frac{\partial J}{\partial w_1}=-3.4\times 2=-6.8$$

• Update Weights :

$$w_0:=0.2-0.1(-3.4)=0.2+0.34=0.54$$ $$w_1:=0.2-0.1(-6.8)=0.2+0.68=0.88$$

Thus, the final model after 1 epoch is :

$$y=0.54+0.88x$$

---

With this post on Linear Regression, normal form equation, gradient descent, types of errors, OLS is over.