LSTM

  • LSTMs were developed to handle the drawbacks of RNNs, i.e., their inability to handle long term dependencies.

  • LSTM are just a special type of RNN which can handle long term dependencies.
  • The repeating module has a different structure as compared to a RNN (as shown in the below figure).

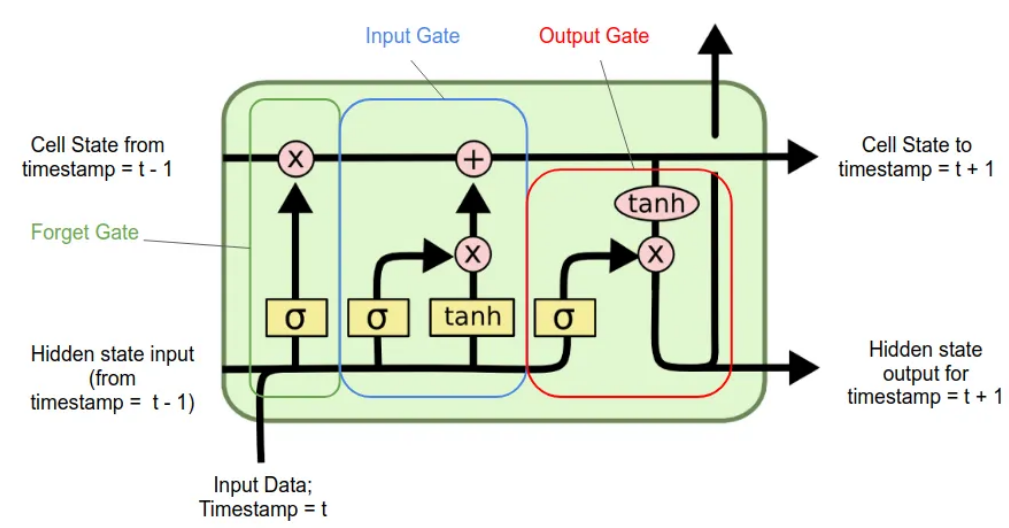
Image

  • red circle : pointwise operation (eg. vector addition)
  • yellow rectangle : neural network layer

  • A simple RNN cell has one main neural layer : \(h_t = tanh(W_{xh}x_t + W_{hh}h_{t-1} + b)\)

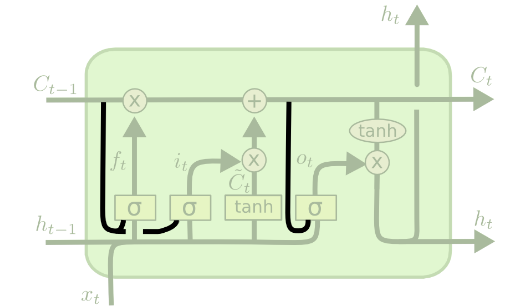
  • LSTM cell consists of 3 gates.

Cell State :

  • It is a vector that acts as the long-term memory of the network.
  • It carries important information across many time steps in a sequence.
  • It is updated / modified only through gates.

Gates of LSTM

1. Forget Gate [ $ f_t $ ]

  • Helps to decide what information is to be thrown away from the cell state.
  • \[f_t = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f)\]

2. Input Gate [ $ i_t $ ]

  • Decides what new information to be stored in the cell state.
  • There are 2 parts in it :

    • Input gate layer :

      • A sigmoid / input gate layer decides which value will be added.
      • $ i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i) $

    • New Memory / Candidate Layer :

      • Proposes new candidate values vector to be added to the cell state using a tanh layer.
      • $ \tilde C_t = tanh(W_C \cdot [h_{t-1}, x_t] + b_C) $
    • These 2 will be combined to get the new cell state update.

3. Update the cell state [ $ C_t $]

  • Updating the cell state from old $ C_{t-1} $ to new $ C_t $.
  • $ C_t = f_t \circ C_{t-1} + i_j \circ \tilde C_t $
  • Multiplying old state by $ f_t $ denotes the forgetting the info which was decided to be forgotten earlier.

4. Ouput Gate [ $ o_t $]

  • Decide which part of the cell state is going to be the output.
  • Done in 2 parts :

    • Deciding the parts going to the output

      • Using a sigmoid layer
      • $ o_t = \sigma (W_o [h_{t-1}, x_t] + b_o) $

    • Get the output

      • Use a tanh layer for values to be in range [-1, 1].
      • $ h_t = o_t \circ tanh(C_t) $

How LSTM solve the Vanishing Grdient Problem

  • The Cell State is the key of the LSTM.

  • Additive updates instead of multiplicative

    • avoids the repeated multiplicative squashing that causes vanishing gradients.
    • $ C_t = f_t \circ C_{t-1} + i_j \circ \tilde C_t $

  • Control Flow of gradients using Forget Gate

    • If $f_t$ = 1 and $i_t$ = 0 then : $C_t = C_{t-1}
    • Thus, the gradient can flow inchanged across many time steps.
    • It provides a highway for gradients to flow.

Variations of LSTM (using peepholes)

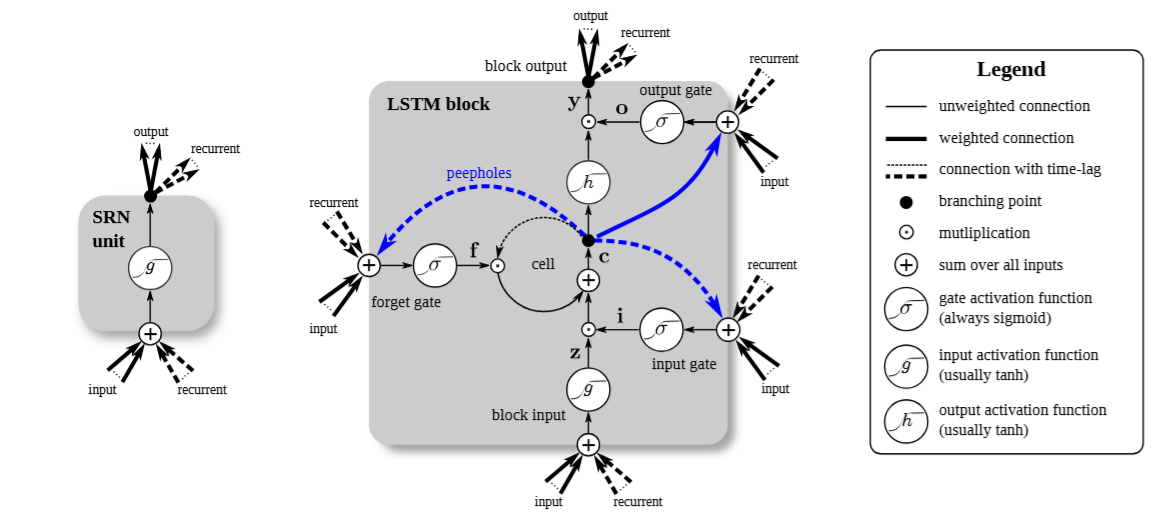
Image

  • All the gates get a direct connection to the previous cell state.
  • Since the cell state $C_{t-1}$ contains richer memory than the hidden state $h_{t-1}$ , allows for more informed decision making.

Updated gate eqautions

  • $ f_t = \sigma (W_f \cdot [C_{t-1}, h_{t-1}, x_t] + b_f) $
  • $ i_t = \sigma (W_i \cdot [C_{t-1}, h_{t-1}, x_t] + b_i) $
  • $ o_t = \sigma (W_o [C_{t-1}, h_{t-1}, x_t] + b_o) $

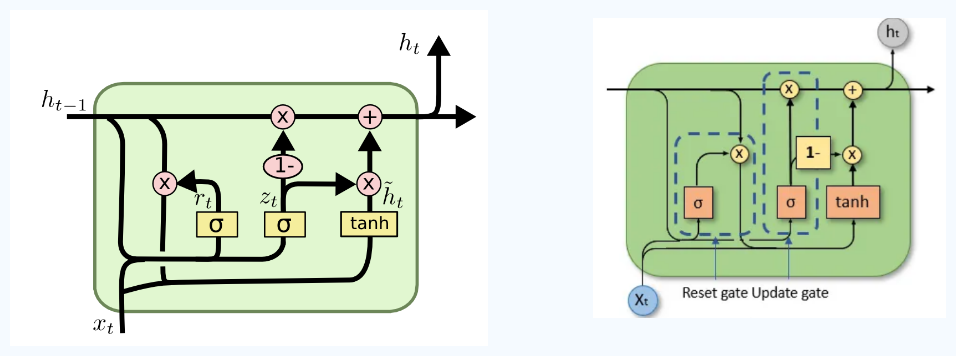
Image

GRU

  • It is a simplified variation of LSTM.
  • It has fewer parameters and simpler architecture.

Image

  • GRU removes the cell state and merges everything into a single hidden state.

  • Combines Input gate and Forget gate into a single Update Gate $z_t$
    • It decides how much of the past to keep vs. how much new info to add.

  • Removed the output gate, thus directly outputs the hidden state.

  • Added a new Reset Gate $r_t$ to control how much past info to forget when computing the new candidate $\tilde h_t$
  • $z_t = \sigma (W_z \cdot [h_{t-1}, x_t])$
  • $r_t = \sigma (W_r \cdot [h_{t-1}, x_t])$
  • $\tilde h_t = tanh(W \circ [r_t * h_{t-1}, x_t])$
  • $h_t = (1 - z_t) * h_{t-1} + z_t * \tilde h_t$
  • GRUs are faster to compute and has fewer parameters.

Implementation of LSTM in a sentiment analysis task can be found here